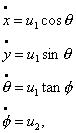
|
MAE 281B
Nonlinear Control |
Prof. M. Krstic |
|
Homework 4 |
Due: May 28, 2002 |
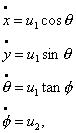
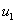 and
and 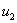 are control inputs ("drive" and
"steer"). The linearization at the origin is obviously not completely controllable (check this!)
By computing
are control inputs ("drive" and
"steer"). The linearization at the origin is obviously not completely controllable (check this!)
By computing 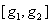 and
and 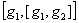 , show that the nonlinear
system is completely controllable.
, show that the nonlinear
system is completely controllable.
 - stabilizable.
- stabilizable.
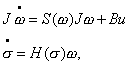
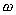 is the angular velocity,
is the angular velocity,
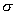 is the attitude (in modified Rodrigues parameters),
is the attitude (in modified Rodrigues parameters),
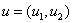 are the torque inputs,
are the torque inputs,

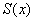 is a skew-symmetric matrix defined as
is a skew-symmetric matrix defined as
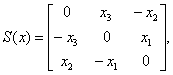
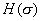 is defined as
is defined as
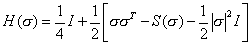 .
.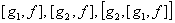 , and
, and 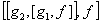 , show that the nonlinear
system is completely controllable whenever
, show that the nonlinear
system is completely controllable whenever 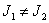 .
.
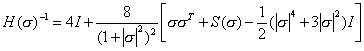 .
.